Mid Point Theorem and Converse of Mid Point Theorem in Triangle

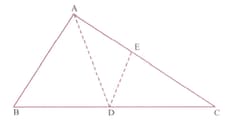
In the adjoining figure, in $∆\mathrm{ABC}$, $\mathrm{AD}$ is the median through $\mathrm{A}$, and $\mathrm{E}$ is the midpoint of $\mathrm{AD}$. If $\mathrm{BE}$ produced meets $\mathrm{AC}$ in $\mathrm{F}$. Prove that $\mathrm{AF}=\frac{1}{3}\mathrm{AC}$.

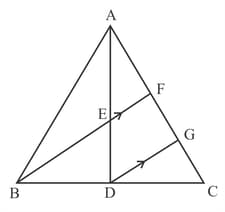
In given figure, $AD$ is a median of $△ABC$ and $E$ is a point on $AC$ such that area ($ADE$) :area ($△ABD$) $=2 :3$. Find $AE : EC$

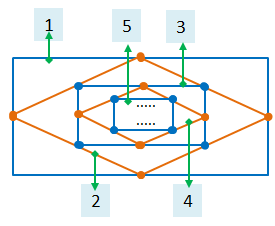
In the design below, assume there are 5 rectangles and 5 rhombuses. The 1st quadrilateral is a rectangle.

Which of the following numbers represents the innermost rectangle?

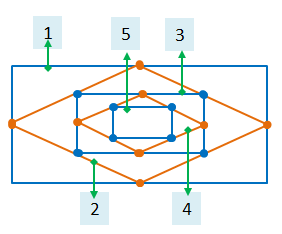
Assume there are 10 quadrilaterals in the design below.

Let $ {\text{A}}_{1}$ and $ {\text{A}}_{9}$ be the areas of the 1st and the 9th quadrilaterals.

Which of these formulae gives the correct relationship between $ {\text{A}}_{1}$ and $ {\text{A}}_{9}$?

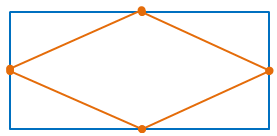
In the figure below, area of the rectangle is ‘A’. The midpoints of its sides are joined to get a rhombus.

What is the area of the rhombus inside the rectangle?

A carpenter is making a table top which is the shape of a right angle triangle by picking one of the pairs of plywood pieces and joining them. (Along the red line)

Which of the following pairs should the carpenter choose to form the table top?

(Note: Figures not to scale. Make your choice based on the measurements only.)